TechStandard

Интерпретация модели (I-компонент теории, interpretation).

На рис.1 приведены экспериментальные точки и графики функции (16), описывающие дрожжевых клеток в присутствии солей хрома и никеля [13]. При расчете графиков брали значения a, b, р , f, определенные по экспериментальным данным [17]. В пределах точности измерений расчетные кривые согласуются с экспериментом при измененении численности примерно на шесть порядков.

Хорошее согласие теории с экспериментом получено и для других биологических объектов [8, 9]. Поэтому интересно провести верификацию квазихимической модели по характеристикам, связанным с проблемами биологического времени.

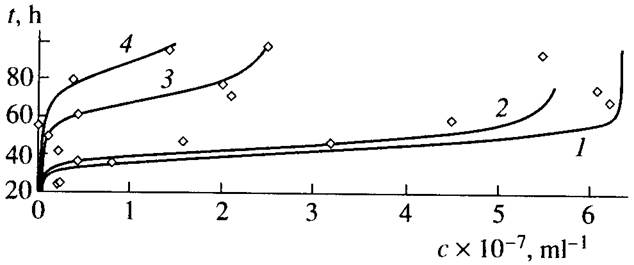
Рис.1. Экспериментальные точки и графики функции (16), описывающие рост пивных дрожжей при разных концентрациях (ммоль/л) солей хрома и никеля [13]: (1) c(Ni) = c(Cr) = 0.0, (2) c(Ni) = 0.5, (3) c(Cr) = 0.5, and (4) c(Ni) + c(Cr) = 0.5 + 0.5. Коэффициенты: a=1.25.10-7 мл /ч, b=0.8ч-1, р=0.32 ч-1, f =2.

Уравнения (12a) можно представить в виде:

где величины Kc1=(-px c1+f b cm+w1) и Kcm= (p c1-bx cm-a c1 cm) представляют собой калибровочные коэффициенты для перехода от интервала физического времени dt к интервалам биологического времени dcj.

На основе (17) получают соотношение между конечными временными интервалами:

Калибровочные соотношения (17) обладают следующими свойствами:

1. Коэффициенты Kc1 и Kcm зависят от кинетических констант, характеризующих внутри- и внесистемные взаимодействия. Это определяет специфику биологического времени данного объекта.

2. Коэффициенты Kc1 и Kcm зависят от наблюдаемого состояния объекта, то есть изменяются при движении по фазовой траектории.

3. Коэффициенты Kc1 и Kcm неодинаковы для однотипных элементов данного уровня иерархии. Это означает, что собственное время «течет» с разной скоростью не только на разных уровнях биологической системы, но и в различных элементах одного уровня.

Приращение суммарной массы dmp или численности dNp популяции определяют интервал биологического времени популяции в целом. Для двухстадийной популяции dNp = V(с1+сm), где V – объем системы. Связь между популяционным и физическим временем согласно (17) определяется соотношением:

Через длительность клеточного цикла tc в физической шкале (в «детлафах») эта величина выразится в виде:

Длительность клеточного цикла tc в физической шкале рассчитывают либо по экпериментальным значениям прироста массы или численности клеток, либо по экпериментальным значениям параметров b и p модели (12).

Приращение численности популяции D с12 =c2-c1 в единице обьема наблюдается за время D t12=t2-t1, согласно (16) равное:

Дополнительно

Счетчики ядерного излучения
Реальная перспектива использования человеком огромных энергий, скрытых в недрах атома, появилась впервые в 1939 году. На сегодняшний день широкое практическое применение получают различного рода ядерные излучения, несмотря на то, что они опасны для организма человека и в то же время неощущаемы, п ...

Внутренняя структура протона и новый способ получения энергии
Протон был открыт в начале 20-х г.г. в экспериментах с альфа-частицами. В опытах по рассеянию на протонах электронов и гамма-квантов были получены достоверные доказательства существования некой внутренней структуры у этой частицы. В 1970 г. в Стенфордском центре линейного ускорителя (СЛАК) удалось ...