TechStandard

Динамические объекты вакуума

Квант в [10,15,25] рассматривается мной как динамическая неоднородность поля, которая возникает при наличии в среде напряженностей электрического Eи магнитного H

полей. Поскольку динамическая неоднородность поля обладает определенными физическими характеристиками, то ее можно рассматривать как физический объект. Исходным для определения физических характеристик динамических объектов вакуума являются векторы напряженности электрического Eи магнитного H

полей. В работе [10] показано, что при равенстве скалярных произведений векторов и их роторов в виде HrotE = E

rotH

, энергия электромагнитного поля локализуется в пространстве в виде кванта.

Рассмотрим подробнее какими физическими характеристиками может обладать динамическая неоднородность поля. Плотность энергии w

электромагнитного поля определяется согласно следующему соотношению [4]:

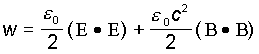(1)

Энергия поля E

в объеме V

с учетом бинарной сущности динамической неоднородности [10,12,13] равна:

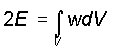(2)

Скорость изменения энергии в данном объеме определяется соотношением:

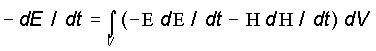(3)

Вместо производных по времени подставим их значения в виде rotE

и

rotH

из уравнений Максвелла. С учетом этого получим:

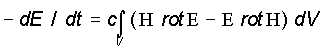(4)

Выражение в скобках есть дивергенция векторного произведения [EхH]

,

поэтому:

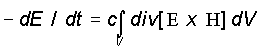(5)

Условием, при котором энергия в данном объеме будет оставаться постоянной, является равенство нулю производной dE/dt

. Из соотношения (5) следует, что производная dE/dt

будет равна нулю при div [ExH]=0

.

Поскольку векторное произведение [ExH]

есть вектор Умова-Пойнтинга:

[ExH] = P, (

6)

то из формулы Остроградского - Гаусса, при нулевой дивергенции, следует:

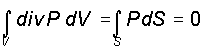(7)

Это означает, что поток вектора Пойнтинга через поверхность S

, ограничивающую

объем V

, равен нулю. Поскольку div [ExH] = 0

, а вектор Пойнтинга не равен нулю, то поток вектора Пойнтинга остается в объеме Vи не выходит за пределы поверхности S

, ограничивающей данный объем.

Исследуем поведение потока вектора Пойнтинга внутри данного объема. Пользуясь теоремой разложения Гельмгольца [5] вектор Пойнтинга Р

можно представить суммой двух составляющих Р

1 и P2из которых одна является вихревой, а другая потенциальной.

P = P1 + P2.

Тогда rotР = rotР1, rotР2 = 0, div P = div P2, div P1 =0

.

Из соотношения (7) следует, что в рассматриваемом нами случае существует только вихревая составляющая вектора Пойнтинга. Из теоремы Стокса следует что:

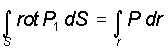(8)

Поток ротора Р

через поверхность S

равен циркуляции вектора Рпо замкнутому контуру. Таким образом, при определенных условиях энергия локализуется в заданном объеме.

В общем случае, когда H rotE <> E rotH

, приходим еще к двум вариантам в поведении энергии внутри динамических объектов вакуума. При H rotE > E rotH

получаем положительное значение дивергенции вектора Пойнтинга div P > 0

. При положительном значении дивергенции вектора Пойнтинга энергия покидает объем, что приводит к уменьшению вихревой составляющей вектора Пойнтинга.

При H rotE < E rotH

получаем отрицательное значение дивергенции вектора

Пойнтинга div P < 0.

При отрицательном значении дивергенции вектора Пойнтинга энергия возрастает в заданном объеме, что приводит к росту вихревой составляющей вектора Пойнтинга и к росту циркуляции вектора. Изменение вихревой составляющей вектора Пойнтинга сопровождается изменением циркуляции вектора, что непосредственно следует из теоремы Стокса. Таким образом, изменение энергии приводит к изменению частотной характеристики динамического объекта вакуума.

Из соотношения (5) непосредственно следует, что скорость изменения энергии тем больше, чем больше величина div P

. При этом, положительному значению divP

соответствует убывание энергии, а отрицательному значению divPсоответствует возрастание энергии. Поскольку энергия и размеры области ее локализации связаны обратной пропорцией [10,13], то отсюда следует, что скорость изменения размеров невещественных динамических объектов поля в пространстве пропорциональна дивергенции вектора Пойнтинга.

Дополнительно

Нетрадиционные методы производства энергии
Рождение энергетики произошло несколько миллионов лет тому назад, когда люди научились использовать огонь. Огонь давал им тепло и свет, был источником вдохновения и оптимизма, оружием против врагов и диких зверей, лечебным средством, помощником в земледелии, консервантом продуктов, технологическ ...

Солнце и его влияние на землю
Каждому наверняка известно, что на Солнце нельзя смотреть невооруженным глазом, а тем более в телескоп без специальных, очень темных светофильтров или других устройств, ослабляющих свет. Пренебрегая этим советом, наблюдатель рискует получить сильнейший ожог глаза. Самый простой способ рассматриват ...