Точные формулы и асимптотика
Начнем с наиболее продвинутой в математическом плане ситуации, когда для статистики известны как предельное распределение, так и распределения при конечных объемах выборки.
Примером является двухвыборочная односторонняя статистика Н.В.Смирнова. Рассмотрим две независимые выборки объемов m и n из непрерывных функций распределения F(x) и G(x) соответственно. Для проверки гипотезы однородности двух выборок
H0 : F(x) = G(x) для всех действительных чисел x
в 1939 г. Н.В.Смирнов в статье [4] предложил использовать статистику
D+(m,n) = sup ( Fm(x) - Gn(x) ) ,
где супремум берется по всем действительным числам x. Для обсуждения проблемы соотношения точных и предельных результатов ограничимся случаем равных объемов выборок, т.е. m = n. Положим
H(n, t) = P ( D+(n,n) $ t n - 1/2) .
В цитированной статье [4] Н,В. Смирнов показал, что при безграничном возрастании объема выборки n вероятность H(n, t) стремится к exp ( - t 2 ).
В работе [5] 1951 г. Б.В.Гнеденко и В.С.Королюк показали, что при целом с = t n1/2 (именно при таких t вероятность H(n, t) как функция t имеет скачки, поскольку статистика Смирнова D+(n,n) кратна 1/ n ) рассматриваемая вероятность H(n, t) выражается через биномиальные коэффициенты, а именно,
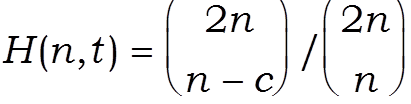(1).
К сожалению, непосредственные расчеты по формуле (1) возможны лишь при сравнительно небольших объемах выборок, поскольку величина n!.уже при n=100 имеет более 200 цифр и не может быть без преобразований использована в вычислениях. Следовательно, наличие точной формулы для интересующей нас вероятности не снимает необходимости использования предельного распределения и изучения точности приближения с его помощью.
Широко известная формула Стирлинга для гамма-функции и, в частности, для факториалов позволяет преобразовать последнее выражение в асимптотическиое разложение, т.е. построить бесконечный степенной ряд (по степеням n ) такой что каждая следующая частичная сумма дает все более точное приближение для интересующей нас вероятности H(x, t) . Это и было сделано в работе А.А.Боровкова [6], опубликованной в 1962 г. Большое количество подобных разложений для различных статистических задач приведено в работах [7-9] В.М.Калинина и О.В. Шалаевского в конце 60-х - начале 70-х годов. (Интересно отметить, что асимптотические разложения в ряде случаев расходятся, т.е. остаточные члены имеют нетривиальную природу.)
В наших работах конца семидесятых годов была сделана попытка теоретически оценить остаточный член второго порядка. Итоги подведены в статье [10] и монографии [11, § 2.2, с.37-45]. Справедливо равенство
H(n, t) = exp ( - t 2 ).(1 + f(t)/n + g(n,t)/ n2 ),
где
f(t) = t2 (1/2 - t2/ / 6 ).
Целью указанных работ было получение равномерных по n, t оценок остаточного члена второго порядка g(n,t) сверху и снизу в области, задаваемой условиями
0 < t n - 1/2 < А, 0 < t < t max , n $ n0 . (2)
С помощью длинных цепочек оценок остаточных членов в формулах, получаемых при преобразовании формулы (1) к предельному виду, сформулированная выше цель была достигнута, и для различных наборов параметров А, t max , n0 получены равномерные по n, t оценки остаточного члена второго порядка g(n,t) сверху и снизу в области (2). Так, например, при А = 0,5, t max = 1,73, n0 = 8 нижняя граница равна (- 0,71), а верхняя есть 2,65.
Основными недостатками такого подхода являются являются , во первых, зависимость оценок от параметров А, t max , n0 , задающих границы областей, во-вторых, завышение оценок, иногда в сотни раз, обусловленное желанием получить равномерные оценки по области (оценкой реальной погрешности в точке является значение следующего члена асимптотического разложения).
Поэтому при составлении рассчитанной на практическое использование методики [12] проверки однородности двух выборок с помощью статистики Смирнова мы перешли на другую методологию (назовем ее "методологией заданной точности"), которую кратко можно описать следующим образом.
а) Выбирается достаточно малое число р, например р = 0,05 или р = 0,20.
б) Приводятся точные значения H(n, t) для всех значений n таких, что
| H(n, t) - exp ( - t 2 ) | > p exp ( - t 2 ) .
в) Если же последнее неравенство не выполнено, то предлагается пользоваться вместо H(n, t) предельным значением exp ( - t 2 ).
Таким образом, принятая нами в методике [12] методология предполагает интенсивное использование вычислительной техники. Результат расчетов - граничные значения объемов выборок n(p,t) такие, что при меньших значениях выброк рекомендуется пользоваться точными значениями, а при больших - предельными, - описывается таблицей, а не формулой. Отметим, что при построении реальных таблиц не обойтись без выбора того или иного конкретного значения р, задающего объемы таблиц.
Дополнительно
Оборудование для механического обезвоживанья и сушки текстильных материалов
Сушка является самым распространенным технологическим
процессом красильно-отделочного производства. На многих отделочных фабриках
сушильное оборудование занимает приблизительно до 30 % производственных
площадей, потребляет до 40 % всего расходуемого тепла и до 30 % электроэнергии.
Одним из эффек ...
Есть ли жизнь на Марсе
«Есть ли жизнь на
Марсе, нет ли жизни на Марсе - науке неизвестно» - это не просто удачный
афоризм из популярной кинокомедии «Карнавальная ночь», который широко вошел в
наш разговорный язык и стал ходячей шуткой. Главное здесь в том, что эта фраза
очень долгое время отражала наш действитель ...