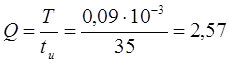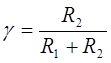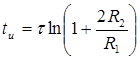TechStandard

Обоснование выбора схемы

Итак, мультивибратор – это релаксационный генератор, вырабатывающий импульсы почти прямоугольной формы. При выборе схемы реализации данного устройства мы будем стараться найти оптимальный вариант между простотой, низкой стоимостью и исходными данными задания.

Найдем скважность генерируемых импульсов:

где Т=0,09 мс – период следования импульсов

tu=35 мкс – длительность выходного импульса

В нашем случае требуется получить генерируемые импульсы большой скважности 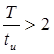, следовательно, цепь заряда конденсатора должна отличаться от цепи разряда.

Выберем схему мультивибратора на ОУ, приведенной на рисунке №1.

В данном случае положительная обратная связь обеспечивается делителем напряжения на резисторах R1, R2.

В момент t=0 (рис.2) включается источник питания ИОУ. При этом начинает возрастать , а следовательно, и напряжение, снимаемое с делителя R1, R2 и поданное на вход , что вызывает дальнейшее увеличение выходного напряжения , т.е. происходит лавинообразный процесс, в результате которого скачкообразно возрастает до значения (это первое состояние квазиравновесия), а - до значения , где

Напряжение при этом практически не изменяется и равно нулю.

С увеличением t за счет заряда конденсатора через резистор увеличивается напряжение по экспоненциальному закону

до значения Е.

В момент времени . При этом уменьшается лавинообразно, меняя полярность на противоположную. В результате окончания этого лавинообразного процесса , а .

Конденсатор начинает разряжаться через резистор и стремится перезарядиться до напряжения .

В момент, когда при перезагрузке конденсатора напряжение достигает значения , вновь возникает регенеративный процесс, завершающийся переключением схемы во второе состояние квазиравновесия.

Таким образом, периодически происходит переход из одного состояния квазиравновесия в другое.

Первый импульс имеет меньшую длительность , т.к он формулируется при зарядке конденсатора от нуля до , и определяется по формуле: , где

Последующие импульсы определяются по формуле:

Дополнительно

Автоматизированное проектирование станочной оснастки
1.1. СТАНОЧНЫЕ ПРИСПОСОБЛЕНИЯ . КЛАССИФИКАЦИЯ , ВИДЫ . 1.1.1. Станочные приспособления . Основную группу технологической оснастки составляют приспособления механосборочного производства. Приспособлениями в машиностроении называют вспомогательные устройства к технологич ...

Современный прокатный стан
Современный прокатный стан представляет собой технологический комплекс последовательно установленных машин, используемых для получения прокатных изделий заданных размеров с необходимыми качественными показателями. Производительность прокатного стана определяется пропускной способностью отдельных а ...