Примеры априорного подхода.
Применение принципа оптимальности к адаптациям жизненного цикла
Большая часть рассматривавшихся до сих пор адаптации касалась либо морфологических, либо физиологических признаков. Между тем такие признаки, как характер морфогенетических процессов, скорости роста, общие размеры, продолжительность жизни и вклад в размножение, также, вероятно, подвергались естественному отбору. Все эти признаки участвуют в том, чтобы довести продукты размножения до такого состояния, в котором они могут воспроизводиться, и их называют признаками жизненного цикла или цикла развития. Со времени первой работы Лей-монта Коула (9) об эволюции жизненного цикла писали много (хорошие обзоры принадлежат Стирнсу (37, 38)).
Здесь в качестве иллюстрации мы рассмотрим количество ресурсов, затрачиваемых родительской особью на продуцирование гамет, и продолжительность пострепродуктивного периода ее жизни. То обстоятельство, что не все организмы бурно размножаются один раз в жизни, заставляет думать, что размножение сопряжено с большими затратами ресурсов. В противном случае приспособленность в неодарвинистском смысле была бы всегда максимизирована путем максимально возможного репродуктивного выхода, а следовательно, путем затраты максимального количества ресурсов на образование гамет. Принято считать, что, чем больше ресурсов данная родительская особь вкладывает в размножение, тем меньше их у нее остается для того, чтобы обеспечить защиту собственного организма от несчастных случаев, болезней и хищников, так что эти расходы можно оценивать в терминах выживаемости родительских особей. В результате с увеличением вклада в репродукцию шансы родителей на выживание в пострепродуктивный период снижаются; здесь мы используем фишеровскую меру приспособленности, то есть г (см. разд. 2.3.2), в сочетании с упрощенным вариантом принципа оптимальности, с тем чтобы исследовать, какого рода компромисс возможен между этими переменными.
Значение приспособленности г можно записать как
где It — выживаемость с момента рождения до времени t, a nt — число потомков, произведенных ко времени t (простой вывод этого уравнения см. у Уилсона и Боссерта (45)). В простейшем случае, когда размножение происходит один раз в год (t=1), плодовитость (п) зависит от возраста и родительские особи выживают после размножения, уравнение 3.1 принимает вид
где 1а и // — соответственно выживаемость взрослых особей и потомков, а п— число потомков на одну родительскую особь. Отсюда
Таким образом, из уравнения 6.6 мы видим, что если построить график зависимости 1а от п, то изоклины равных г будут иметь вид прямых с наклоном, равным — l1 (рис. 3.3.).
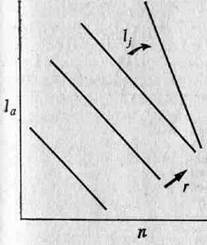
Рис. 3.3. На графике зависимости 1а от п изоклины т представляют собой прямые линии с отрицательными наклонами //. По мере увеличения выживаемости потомков наклон возрастает. В принципе приспособленность, то есть г, возрастает с увеличением la и п.
Однако вследствие компромисса между выживаемостью родительских особей и размножением не все комбинации 1а с п реально осуществимы. Можно представить себе некоторое число распределений реально возможных величин; одно из них показано на рис. 3.4. Здесь выживаемость взрослых особей снижается все быстрее, по мере того как все больше ресурсов вкладывается в размножение, то есть производится все больше гамет.
С помощью этих распределений нетрудно найти оптимальное решение: это та реально осуществимая комбинация 1а и п, которая лежит на самой высокой r-изоклине, то есть максимизирует г, или приспособленность. Для «компромиссной кривой», изображенной на рис. 3.4, этот оптимум приходится на крайнюю правую часть кривой; в этом случае отбор благоприятствует высокому уровню репродукции за счет родительской особи. Такой тип размножения называют семелопарией — родительская особь дает потомство один раз, после чего гибнет подобно лососю.
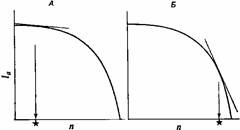
Рис. 3.4. Возможная форма истинной зависимости между 1а и п. А. Выживаемость потомков (//) низкая, "и поэтому отбор благоприятствует небольшому п (оптимум помечен звездочкой) при продолжительном выживании взрослых особей (высокое 1а). Значение // высокое, и поэтому отбор благоприятствует высокому п при низком 1а. Ситуация А ведет к итеропарии, а ситуация Б — к семелопарии (см. текст).
При альтернативном типе размножения, когда достигается некий компромисс между п и 1а, отбор благоприятствует многократному размножению, или итеропарии.
Дополнительно
Технология производства мяса гусей
Животноводство - вторая
важнейшая отрасль сельского хозяйства. Она обеспечивает население
высокобелковыми и диетическими продуктами питания, а ряд отраслей промышленности
- сырьем. Особенность ее в том, что энергоемкость продукции животноводства
(затраты энергии на одну калорию продукции) в 15-2 ...
Становление детской журналистики и её влияние на психологию ребёнка
Русская пресса для юного читателя в
отличие от «взрослой» началась с журнала.
Детская журналистика в нашей стране
имеет богатую историю. До революции, в основном в Петербурге и Москве,
издавалось около трехсот детских и юношеских журналов. Одни из них выходили
десятилетиями, другие прекращали ...