Вращающиеся и заряженные черные дыры
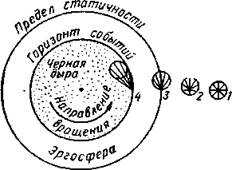Рис. 4. “Вид сверху” по оси вращения на вращающуюся черную дыру. Малые окружности соответствуют положениям фронта волны излучения через малый промежуток времени после испускания волны в точках /, 2, 3, 4. Эффект увлечения в эргосфере настолько велик, что никакое физическое тело не может в ней покоиться относительно удаленного наблюдателя
ла приобретают одну и ту же угловую скорость вращения, равную OMEGA=(J/M)[R2g +(J/Мс)2]-1. Эта величина получила название угловой скорости вращения черной дыры. OMEGA постоянна на поверхности черной дыры. В этом смысле вращение черной дыры напоминает вращение твердого тела. Так же как и при коллапсе невращающегося тела, возрастающее красное смещение при приближении поверхности тела к горизонту и падение по экспоненциальному закону мощности излучения, выходящего к отдаленному наблюдателю, приводят к тому, что через характерные времена порядка Rg /c перестает выходить наружу информация и образуется черная дыра. Заряженные черные дыры. Если коллапсирующее тело обладало электрическим зарядом, то возникающая черная дыра “помнит” об этом. Падение электрического заряда Q в черную дыру приводит к тому, что поток электрического поля через ее поверхность оказывается равным 4piQ в полном соответствии с теоремой Гаусса. Силовые линии электрического поля выходят из черной дыры, и вне ее имеется электрическое поле. Если черная дыра не вращается, то это поле описывается законом Кулона. Вращение заряженной черной дыры с массой М и угловым моментом J приводит к дополнительному появлению дипольного магнитного поля, причем магнитный момент оказывается равным: мю= (Q/M)J. Соответствующее точное решение уравнений Эйнштейна, обобщающее решение Керра на случай, когда черная дыра обладает электрическим зарядом, было получено в 1965 г. в работе группы американских теоретиков во главе с профессором Эзрой Ньюмапом. Как выяснилось позднее, это решение, получившее название решения Керра—Ньюмана, однозначно определяемое тремя параметрами: М - массой, J — угловым моментом и Q —электрическим зарядом, является самым общим из возможных решений, описывающих стационарную черную дыру в пустоте. Геометрические свойства керр-ньюмановской черной дыры весьма сходные с описанными выше свойствами керровской черной дыры.
Поверхность черной дыры при наличии вращения перестает иметь сферическую форму. Площадь поверхности керр-ньюмановской черной дыры равна
A = 4pi [R2g + (J/Mc)2] =4piG2с-4(2M2—Q2/G+.
+ 2Мsqrt[M2—Q2/G—J2c2/G2M2]).
При описании свойств черных дыр важную роль играет так называемая поверхностная гравитация kappa
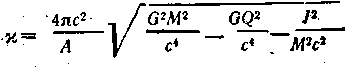
При отсутствии вращения и заряда kappa=c4/GM=GM/R2g Эта величина хaрактеризует “напряженность” гравитационного поля на поверхности черной дыры. Электрический потенциал на поверхности черной дыры равен
Дополнительно
Оборудование для механического обезвоживанья и сушки текстильных материалов
Сушка является самым распространенным технологическим
процессом красильно-отделочного производства. На многих отделочных фабриках
сушильное оборудование занимает приблизительно до 30 % производственных
площадей, потребляет до 40 % всего расходуемого тепла и до 30 % электроэнергии.
Одним из эффек ...
Крепление резины к металлам
С развитием техники, созданием новых машин и аппаратов
появилась потребность в деталях, совмещающих механические свойства металлов с
вибростойкостью, прочностью на истирание, антикоррозионной стойкостью и другими
свойствами, присущими резиновым смесям. Таким образом возникла задача прочного
и надё ...