Обобщенное золотое сечение и теория времени
Очевидно, решения уравнений (5) и (6) существуют при любых s, однако для начала ограничимся рассмотрением 
при 
. Значения для s от 0 до 31 приведены в таблице 1 и в графическом виде на рисунке 1.
Таблица 1
|
s |
|
s |
|
|
0 |
0,50000000000 |
16 |
0,88191004828 |
|
1 |
0,61803398875 |
17 |
0,88624516859 |
|
2 |
0,68232780383 |
18 |
0,89022556753 |
|
3 |
0,72449195900 |
19 |
0,89389541191 |
|
4 |
0,75487766625 |
20 |
0,89729162218 |
|
5 |
0,77808959868 |
21 |
0,90044532576 |
|
6 |
0,79654435413 |
22 |
0,90338297001 |
|
7 |
0,81165232003 |
23 |
0,90612718508 |
|
8 |
0,82430056323 |
24 |
0,90869746041 |
|
9 |
0,83507904272 |
25 |
0,91111068059 |
|
10 |
0,84439752879 |
26 |
0,91338155389 |
|
11 |
0,85255071449 |
27 |
0,91552295788 |
|
12 |
0,85975667169 |
28 |
0,91754622045 |
|
13 |
0,86618067237 |
29 |
0,91946135001 |
|
14 |
0,87195053878 |
30 |
0,92127722540 |
|
15 |
0,87716686945 |
31 |
0,92300175350 |
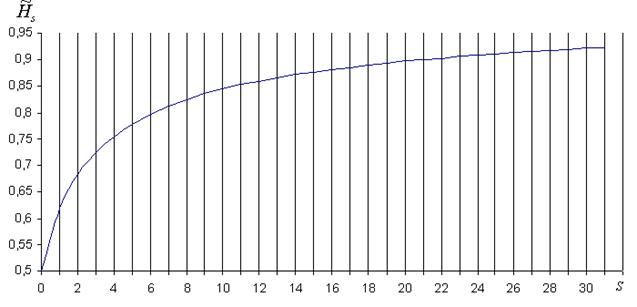рис. 1
Как видно из таблицы 1, 
, то есть при нулевом значении s достигается полное равновесие между двумя частями Единого Целого, то есть состояние полной свободы. При s=1 значение равно обыкновенному Золотому Сечению:
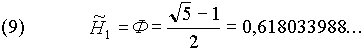
Поэтому соотношения (5) и (6) получили название Обобщенного Золотого Сечения (ОЗС). Мы не будем вдаваться в философско-мировоззренческий смысл Золотого Сечения, который подробно освещен в большом количестве работ [см. например 1, 7, 8]. Отметим лишь тот факт, что исторически оно имеет огромное значение в изучении свойств живой (самоорганизующейся) материи.
Дальнейшее развитие идеи ОЗС приводит нас к построению функции
Выражая s через R и 
и используя (3), получаем
Подставляя полученное выражение для s в (10), находим окончательный вид функции 
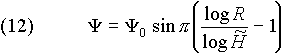
где 
.
Итак, мы построили такую функцию , что ее нули представляют собой наиболее гармоничные, равновесные состояния. Теперь необходимо определить границы качественных переходов, то есть точки максимальной дисгармонии системы, когда никакое равновесие невозможно. Очевидно, такими точками будут являться экстремумы функции . Из этого следует, что ряд 
при является рядом структурной дисгармонии. Он будет определять "зеркальные грани", переход через которые будет означать резкую перемену качества, смену структурно-функционального состояния. В рамках данной работы в виду ее ограниченного объема не имеет особого смысла подробно рассматривать этот ряд, однако без его упоминания описание методов структурного анализа выглядело бы незаконченным.
Дополнительно
Технология производства мяса гусей
Животноводство - вторая
важнейшая отрасль сельского хозяйства. Она обеспечивает население
высокобелковыми и диетическими продуктами питания, а ряд отраслей промышленности
- сырьем. Особенность ее в том, что энергоемкость продукции животноводства
(затраты энергии на одну калорию продукции) в 15-2 ...
Специфика работы секретаря
Специфика работы секретаря
заключается в том, что
ему приходится не только выполнять операции с неодушевлёнными
предметами труда (документы,
технические средства), но и осуществлять многочисленные
контакты с людьми:
руководителем, сотрудниками,
посетителями, телефонными абонентами. Следует уч ...