Принцип эквивалентности и законы сохранения
Рассмотрена ситуация, для которой принятие условия эквивалентности инертной и гравитационной масс приводит к явному конфликту с законом сохранения энергии. Предложена альтернатива классическому принципу эквивалентности.
“ .пропорциональность между инертной и тяжелой массой соблюдается без исключения для всех тел с достигнутой до настоящего времени точностью, так что впредь до доказательства обратного мы должны предполагать универсальность этой пропорциональности .”
А. Эйнштейн, 1, с.95-96
1. ВВОДНАЯ ЧАСТЬ
Истоки принципа эквивалентности тяжелой и инертной масс (ПЭ) восходят к исследованиям Галилея, который получил экспериментальные и нашел логические обоснования следующему результату: ускорение пробного тела в процессе свободного падения (в отсутствие трения) не зависит ни от веса тела, ни от его состава и внутреннего строения. Со временем данное положение обрело значение фундаментального физического принципа, постулирующего эквивалентность (строгое равенство) величин инертной и гравитационной масс для любых пробных тел и частиц.
Большинство современных теорий включают ПЭ в систему своих исходных постулатов, полагаясь на его корректность даже в спецрелятивистском пределе, то есть применительно ко всем компонентам полной массы пробных тел. В общей теории относительности ПЭ также учитывается без каких-либо ограничений. Более того, эйнштейновская формулировка ПЭ предполагает его "усиление" двумя положениями - принципом общековариантности [1, с.456 и фундаментальным для идеологии ОТО постулатом об идентичности "поля ускорения" полю тяжести [1, с.227]. Оба дополнительных положения при скрупулезном рассмотрении обнаруживают свою несостоятельность; об этом достаточно говорилось 2 - 7 .
В настоящей работе, на основе анализа мысленных экспериментов, сделана попытка показать существование границ применимости ПЭ в его исходной, т.н. “классической” формулировке. До настоящего времени претензии к классическому ПЭ не имели принципиального характера.
2. ОСНОВНАЯ ЧАСТЬ
2.1. Существо конфликта ПЭ с законом сохранения энергии
Конфликт между ПЭ и законом сохранения энергии весьма наглядно проявляет себя в следующем мысленном эксперименте.
Ситуация 1. Пусть пробное тело массой m свободно падает в гравитационном поле. Начальный уровень падения обозначим уровнем А. На уровне В находится идеально упругая пружина, о которую ударится это тело. Кинетическая энергия, которой обладало тело до момента взаимодействия с пружиной, при взаимодействии с пружиной переходит в энергию деформации пружины. Энергию, запасенную пружиной в момент полной остановки тела, обозначим как Е1 .
Ситуация 2. Это же тело m медленно опускается на нити с уровня А на уровень В. Предположим, что другой конец нити связан с неким устройством, аккумулирующим всю энергию, выделяющуюся при опускании тела. КПД устройства положим равным единице. При опускании тела до уровня В устройством будет запасена энергия, величина которой относительно уровня В составит Е2 .
Так как начальные и конечные состояния и положения тел в ситуациях 1 и 2 совпадают, мы вправе ожидать равенства величин E1 и E2 - очевидного требования, вытекающего из закона сохранения энергии.
Энергия, как известно, является интегралом силы mg по пути s движения тела, т.е.
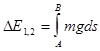, (1)
где g - напряженность гравитационного поля.
В первой ситуации тело проходит каждый элемент пути АВ с большей скоростью, следовательно, характеризуется большей полной массой m, превосходящей полную массу пробного тела во второй ситуации (на величину кинетической составляющей m, принимающей определенное значение для каждого элементарного участка траектории). Отсюда, согласно ПЭ, быстро движущееся тело должно испытывать большую силу гравитационного притяжения, чем аналогичное неподвижное или медленно движущееся. Следуя этим соображениям, напрашивается вывод о превосходстве величины энергии Е1 над величиной Е2 в рассмотренных ситуациях. Данный результат не может быть согласован с законом сохранения энергии, ибо предсказывает появление “из ниоткуда” избытка энергии в каждом цикле “свободное падение тела - его медленный подъем” (равно как “исчезновение” энергии в цикле “медленное опускание тела - его быстрый подъем”).
Требование со стороны закона сохранения энергии применительно к рассмотренному случаю выражается в следующем: максимальная энергия, которая может быть высвобождена в результате перемещения тела, определяется разностью гравитационных потенциалов начальной и конечной точек траектории тела, вне зависимости от характера перемещения тела (свободное падение тела, либо его перемещение с постоянной скоростью).
Дополнительно
Крепление резины к металлам
С развитием техники, созданием новых машин и аппаратов
появилась потребность в деталях, совмещающих механические свойства металлов с
вибростойкостью, прочностью на истирание, антикоррозионной стойкостью и другими
свойствами, присущими резиновым смесям. Таким образом возникла задача прочного
и надё ...
Шероховатость поверхности и её изображение на чертежах
КОНСТРУКЦИЯ
(объект производства)
ТЕХНОЛОГИЯ
(производственные
процессы)
↔
↔
↔
↑ ↑ ↑ ↑
↑ ↑ ↑
...