Принцип эквивалентности и законы сохранения
F0 ~ 22 r . (2)
Чтобы определить, во сколько раз действие гравитационного поля сильнее на совокупность горизонтально ориентированных осцилляторов, чем на ту же их совокупность, но равномерно ориентированную по всем трем пространственным направлениям (2), распределим всю площадь сферы S по плоскости, перпендикулярной плоскости (при этом cos = 1), и найдем гравитационную силу для этого случая:
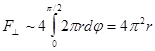. (3)
Из сопоставления (2) и (3) следует коэффициент, равный двум. Это означает, что горизонтально ориентированная ( = 0) составляющая mkin испытывает двойное влияние гравитационного поля (имеет гравитационную массу, вдвое превышающую инертную).
Полученный результат вполне закономерен, если обратить внимание на возможность разложения составляющих движения фотона-осциллятора по трем ортогональным пространственным направлениям x, y, z. Одно из них - m(X) - совпадающее с вектором напряженности поля, два других - m(Y) и m(Z) - перпендикулярны ему. Гравитационное поле трансформирует в m(X) как m(Y) , так и m(Z) ; действие поля на обе поперечные составляющие закономерно приводит к двойному искривлению горизонтального участка траектории фотона.
Под действием гравитации фотон меняет траекторию движения, но его энергия при этом не изменяется. Как известно, энергия фотона жестко связана с величиной его полного импульса. Импульс фотона соответственно остается неизменным по величине, хотя меняется его ориентация. Соответственно проекция импульса фотона на первоначальное направление уменьшается.
Таким образом, инертная масса фотона полностью определяется его кинетической массой, а гравитационная масса фотона m gr в поле тяжести является функцией ориентации движения фотона относительно вектора напряженности g-поля:
m gr = 2m in sin , (4)
где sin является коэффициентом, определяющим проекцию скорости фотона на вектор напряженности g-поля. Гравитационная масса фотона равна его инертной массе лишь при определенном значении угла : = 30 .
Выводы, которые сформулированы для фотона (исходя из принятого постулата о единообразии всех форм материи-массы на самом элементарном уровне), не имеют видимых противопоказаний к их распространению на кинетическую составляющую массы тел с ненулевой массой покоя.
Выражение для мгновенной величины силы гравитационной природы Fg , действующей на тело с полной массой m (m = m0 + mkin), с учетом соотношений (3) и (4), запишется так:
Fg = m0 g + 2mkin g sin , (5)
где g - величина напряженности гравитационного поля. При этом величина (m0 + 2mkin) соответствует поперечной гравитационной массе, а величина m0 - продольной гравитационной массе тела.
В соответствии с (5) при , большем 30, на тело будет действовать большая гравитационная сила, чем предписывается ПЭ (гравитационная масса оказывается больше инертной, приводя к большей кривизне траектории); при 30 соответственно меньшая гравитационная сила.
Данный вывод может быть экспериментально проверен с участием быстрых частиц в гравитационном поле. Кривизна горизонтального участка траектории любой субсветовой частицы (ускоренного электрона, протона, нейтрона), для которой выполняется условие m m0 , в поле тяжести предполагается почти вдвое большей, чем предсказывается теориями гравитации, безусловно поддерживающими справедливость классического ПЭ.
Ключевые положения следующего за ОТО уровня проникновения в сущность гравитации вполне могут быть такими:
1. В общем случае гравитационная масса (гравитационный заряд) тела не равна его инертной массе. Гравитационной массой определяется взаимодействие тела с g-полем, а инертной массой - способность транспортировать энергию в пространстве.
2. Стационарное g-поле не способно изменить ни полную массу, ни полную энергию свободно падающего тела. В гравитационном поле лишь перераспределяются энергетические составляющие полной энергии тела, характеризующие его исходное состояние и меняется импульс тела.
3. Фотон есть первооснова вещества, обладающего инертными свойствами (постулат о единстве состава материи на уровне первомассы 8 ).
2.4. Континуумальная кривизна и сохранение импульса
Почти девять десятков лет минуло с той поры, когда А. Эйнштейн поделился с мировым сообществом мыслью о том, что гравитация есть результат континуумальной кривизны 1, с.227-236 . Чуть позже оказалось, что идею метрической кривизны можно привлечь для объяснения более широкого круга явлений, чем это позволяла теория тяготения Ньютона. Среди этих явлений особое место занимают наблюдаемое вращение орбиты Меркурия, а также аномально большее искривление траектории света в гравитационном поле сильногравитирующего объекта (Солнца) [1, с.439-447].
Дополнительно
Лазерная система для измерения статистических характеристик пространственных квазипериодических структур
В последние годы наблюдается интенсивное развитие аэрокосмической и ракетной
техники, что в свою очередь ставит перед промышленностью задачу создания точных
и надежных систем связи, ориентации и обнаружения подвижных объектов в
пространстве. В большинстве случаев данные задачи решаются с прим ...
Становление детской журналистики и её влияние на психологию ребёнка
Русская пресса для юного читателя в
отличие от «взрослой» началась с журнала.
Детская журналистика в нашей стране
имеет богатую историю. До революции, в основном в Петербурге и Москве,
издавалось около трехсот детских и юношеских журналов. Одни из них выходили
десятилетиями, другие прекращали ...