Математическая модель квазипериодической структуры СВЧ линий замедления
Поскольку ширина ![]() щелей и
щелей и ![]() стенок являются величинами случайны-ми и взаимонезависимыми, то и период
стенок являются величинами случайны-ми и взаимонезависимыми, то и период ![]() пространственной структуры ЛЗ будет также величиной случайной. Период
пространственной структуры ЛЗ будет также величиной случайной. Период ![]() является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения
является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения ![]() также будет нормальным.
также будет нормальным.
Таким образом, амплитудный коэфициент пропускания ![]() прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
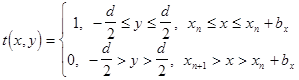 (2.4), где
(2.4), где ![]() - порядковый номер щели,
- порядковый номер щели, ![]() - пространственная координата положения начала щели,
- пространственная координата положения начала щели, ![]() - высота перекрытия зубьев в квазипериодической структуре ЛЗ.
- высота перекрытия зубьев в квазипериодической структуре ЛЗ.
Из выражения (2.4) видно, что переменные х и у функции ![]() взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций
взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций ![]() и
и ![]() , т.е.
, т.е. ![]() (2.5).
(2.5).
В выражении (2.5) функция ![]() является финитной в пределах высо-ты
является финитной в пределах высо-ты ![]() перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
Для оптической системы КОС пространственная структура ЛЗ является квазипериодическим сигналом. В свою очередь, основными характеристи-ками такого сигнала, т.е. пространственной структуры ЛЗ, являются:
· средние размеры ![]() и
и ![]() ширины стенок и щелей, а также средние квадратические отклонения СКО
ширины стенок и щелей, а также средние квадратические отклонения СКО ![]() и
и ![]() от них соответственно;
от них соответственно;
· законы распределения ![]() и
и ![]() размеров стенок и щелей;
размеров стенок и щелей;
· спектральная и корреляционная функции.
Для описания спектральных и корреляционных функций случайных сигналов часто используются характеристические функции. Характеристи-ческая функция ![]() случайной величины
случайной величины ![]() является фурье-образом ее закона распределения
является фурье-образом ее закона распределения ![]() , т.е.
, т.е. 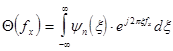 , где
, где ![]() - простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата
- простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата ![]() является пространственной и имеет размерность [мм].
является пространственной и имеет размерность [мм].
Тогда с учетом 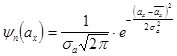 получим:
получим:
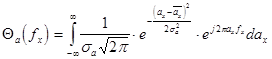 , а вводя замену переменных вида
, а вводя замену переменных вида
![]() . Этот интеграл в новых пределах интегрирования от
. Этот интеграл в новых пределах интегрирования от ![]() до
до ![]() можно представить через элементарные функции следующим выражением
можно представить через элементарные функции следующим выражением
Дополнительно
Расчет релаксационного генератора на ИОУ
Разработать и рассчитать
релаксационный генератор на ИОУ
(интегральной схеме операционного
усилителя) в соответствии с данными, представленными:
·
вид генератора - мультивибратор
·
режим работы – автоколебательный
·
период следования импульсов Т, мс – 0.09
· ...
Высокопроизводительная, экономичная и безопасная работа технологических агрегатов металлургической промышленности
Высокопроизводительная,
экономичная и безопасная работа технологических агрегатов металлургической
промышленности требует применения современных методов и средств измерения
величин, характеризующих ход производственного процесса и состояние
оборудования. Автоматический контроль является логически ...