Математическая модель квазипериодической структуры СВЧ линий замедления
(2.6) , и аналогично 
(2.7).
Полученные выражения (2.6) и (2.7) являются характеристическими функциями квазипериодической пространственной структуры ЛЗ с нормаль-ным законом распределения ширины 
стенок и 
щелей.
Как в оптических, так и в электронных устройствах спектрального анали-за сигналов, существует возможность получения как амплитудного, так и энергетического их спектров. Однако в теории спектрального анализа пространственных сигналов известно, что при использовании квадратичес-ких фотодетекторов для регистрации параметров дифракционного изобра-жения, формируемого оптической системой КОС, автоматически на ее вы-ходе формируется энергетический спектр исследуемого сигнала. Парамет-ры такого спектра могут быть измерены соответствующими контрольно-измерительными приборами, а форма его определена с применением мето-дов статистической радиооптики путем интегрального преобразования Винера-Хинчина, либо на основе теоремы Хилли.
Поэтому используя аналогию математических методов исследования спектральных характеристик пространственных и временных сигналов, распределение комплексных амплитуд спектра пропускания 
в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как 
, или с уче-том (2.5) 
.
Полученное выражение описывает амплитудный спектр функции пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр 
этой функции может быть определен с помощью теоремы Хилли [3.11] как 
, или же
.
Однако в работах [16, 17] показано, что для квазипериодического сигнала, описываемого единично-нулевой функцией вида (2.4)
(2.8), где 
- дискретная составляющая спектра на нулевой частоте, которая для квазипериодической структуры ЛЗ будет равна
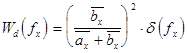(2.9) , а 
- непрерывная составляющая спектра, равная: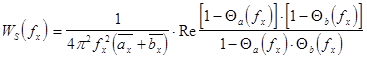 
(2.10), что справедливо для 
и 
не равных 1, согласно [3.35].
В выражениях (2.9) и (2.10) параметр 
является пространственной частотой энергетического спектра исследуемого сигнала, величина которой определяется коэфициентом 
масштаба и зависит от схемы построения и геометрических размеров оптической системы КОС.
Для определения формы энергетического спектра пространственной структуры ЛЗ рассмотрим вещественную часть комплексной дроби в выражении (2.10), обозначив ее через В, т.е.
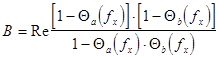(2.11). Подставив в (2.11) выражения (2.6) и (2.7) характеристических функций и получим:
Дополнительно
Методы оценки близости допредельных и предельных распределений статистик
Рассматривается проблема оценки близости предельных
распределений статистик и распределений, соответствующих конечным объемам
выборок. При каких объемах выборок уже можно пользоваться предельными
распределениями? Каков точный смысл термина "можно" в предыдущей фразе?
Основное внимание уд ...
Кибернетика и синергетика – науки о самоорганизующихся системах
Фронт современной науки простирается от
сравнительно частных, конкретных концепций относительно различных областей
физического и химического мира, до глубочайших теорий, охватывающих различные
сферы природы, общества и технической деятельности человека. К последним
следует отнести кибернетику и ...