Расчет на изгиб пластинчатых упругих элементов, расположенных в плоскости, перпендикулярной оси ступицы
Е — модуль продольной упругости материала;
— приведенная гибкость стержня при продольном изгибе;
imin — наименьший радиус инерции поперечного сечения;
m — коэффициент приведённой длины;
l — длина стержня (рессоры).
В общем случае сжатого монолитного стержня (рессоры) критическая сила определяется как:
|
,
где Jmin — наименьший из главных центральных моментов инерции сечения
l — полная длина стержня;
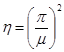— коэффициент критической нагрузки.
Коэффициенты h и m зависят от способа закрепления торцовых и промежуточных сечений рессоры, характера её нагружения продольными силами, закона изменения сечения стержня по длине.
Для рессор постоянного сечения, нагруженных продольными силами, приложенными к их торцевым сечениям, коэффициент h зависит только от условий закрепления концов рессоры. При сжатии рессоры с эксцентриситетом в пределах упругих деформаций наблюдается сложная нелинейная зависимость между напряжениями и сжимающей силой. Величина эксцентриситета е влияет на быстроту нарастания деформаций: чем больше эксцентриситет, те быстрее нарастают прогибы при увеличении сжимающей силы Р.
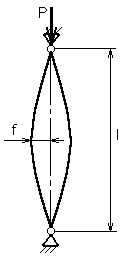
Рассмотрим рессору, шарнирно закреплённую на концах (см. рисунок 4.2).
Если сжимающие силы приложены на концах с эксцентриситетом е, прогиб посредине стержня приближенно равен:
|
, где 
Если сжимающая сила Р стремится к эйлеровой критической силе, 
, прогиб быстро возрастает. Если до загружения стержень (рессора) имела начальное искривление, которое приближенно можно считать синусоидой с одной полуволной и амплитудой f0, то при действии продольной силы Р дополнительный прогиб посредине будет равен:
|
В этом случае прогиб также неопределённо возрастает, если сжимающая сила приближается к критическому значению.
Исходя из сказанного выше, применительно к нашей задаче можно сказать, что критическая сила для конической консольной балки может быть вычислена по формуле (4.16) как
|
Дополнительно
Конструкции и технология изготовления электротехнических изделий
Настоящее методическое
пособие предназначено для студентов Института Электротехники, выполняющих
курсовые и дипломный проекты (КП и ДП), и призвано оказать им помощь по
выполнению конструкторско-технологической части проектов.
В связи с введением Единой
системы конструкторской документации (ЕСК ...
Современный прокатный стан
Современный
прокатный стан представляет собой технологический комплекс последовательно
установленных машин, используемых для получения прокатных изделий заданных
размеров с необходимыми качественными показателями. Производительность
прокатного стана определяется пропускной способностью отдельных а ...