TechStandard

Расслоенные пространства внутренних степеней свободы

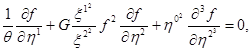
где - безразмерная постоянная, – диэлектрическая проницаемость. Она является безразмерной величиной. Если же среда анизотропная, то диэлектрическую проницаемость могли составлять величины . Ограничимся классом решений , где , то есть . Тогда одним из решений данного уравнения будет являться функция

Построим функцию следующим образом:

, где .

Тогда нелинейные дифференциальные уравнение для L и F2 представляется в форме:

Каждое дифференциальное уравнение индуцирует соответствующей структуры пространство [ 3 ]. В данном случае решение дифференциального уравнения сводится к поиску геометрических структур данного пространства

.

Введем обозначение

В выделенном классе решений получаем следующие дифференциальные уравнения слоевых координат пространства :

Имеем и следующие значения слоевых координат (составляющие ковариантного вектора ):

, где .

Проверим правильность нахождения векторов . Должно иметь силу соотношение . Имеем

Составляющие определены правильно.

В рассматриваемом классе решений получаем следующие нелинейные дифференциальные уравнения для составляющих метрического тензора :

.

Тогда составляющие коэффициентов связностей находится по формулам:

В итоге получаем составляющие метрического тензора

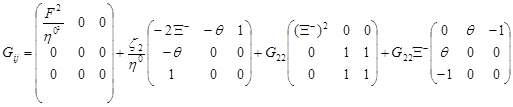
И составляющие коэффициентов связностей:

, ,

.

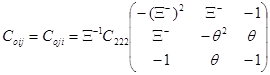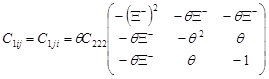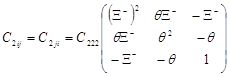Проверка правильности найденных составляющих метрического тензора производится традиционным способом, а именно, в выражение следует подставить конкретные значения для составляющих метрического тензора и получить квадрат метрической функции. Подстановка в данное выражение найденных здесь составляющих метрического тензора приводит

Дополнительно

Технология выращивания сахарной свеклы в Сумской области
Сахарная свекла - важная техническая культура, корнеплод которой достигает 500г и больше, содержит 19-22% сахара и более, является основным сырьем для сахарной промышленности. Кроме сахара, в процессе переработки корнеплодов получают ценные дополнительные продукты - мелясу и жом. Ботва сахарной св ...

Кибернетика и синергетика – науки о самоорганизующихся системах
Фронт современной науки простирается от сравнительно част­ных, конкретных концепций относительно различных областей физи­ческого и химического мира, до глубочайших теорий, охватывающих различные сферы природы, общества и технической деятельности че­ловека. К последним следует отнести кибернетику и ...