Расслоенные пространства внутренних степеней свободы
к квадрату метрической функции.
Проверка правильности найденных здесь составляющих связностей производится посредством достижения выполнения условия Эйлера
.
Найденные здесь значения метрического тензора приводят
к выполнению данного условия .
Определим коэффициенты
.
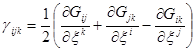Поставим конкретные значения для составляющих метрического тензора. Получаем
| |
,
, 
.
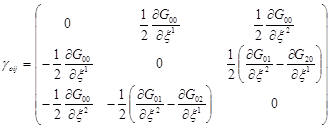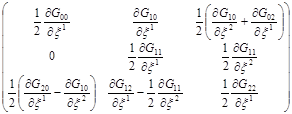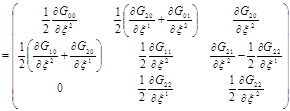Составляющие этих матрицы сводятся к 
, 
и 
. Используя производные от этих величин, получаем конкретные значения 
:
, 
.
Определим величины 
, входящие в уравнение геодезических, по формуле [ 2 ]:
Имеем
Используя формулы:
Получаем для 
и 
:
Правильность введенных здесь значений для 
и можно проверить, если выполняется условие
Такое тождество выполняется
при подстановке конкретных значений.
Определим коэффициенты 
и 
[ 2 ].
Существует связь [ 2 ]
Если 
, тогда
.
Речь идет о параллельном переносе составляющих вектора 
. Имеем
=
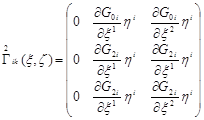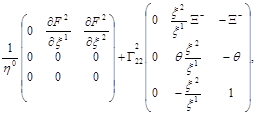
где 
В введенном пространстве могут быть определены переносы тензоров более высокого ранга по формулам, которые приведены в работах [ 1, 2 ].
Заключение.
Построенные здесь геометрические структуры расслоенного пространства внутренних степеней свободы, ассоциируемого с термоэлектрическим состоянием. Возможно многообразие других термоэлектрических состояний. Речь идет о методе
построения геометрических структур, об “офизичивании” геометрии расслоенных пространств. Привлечение в физику расслоенных пространств позволяет построить весьма корректно теории сложных физических систем с большой неоднородностью и анизотропией, с большой нелинейностью и находящихся в сильных физических полях.
Дополнительно
Ремонт колесных пар
Из-за больших
статических и динамических нагрузок, которые возникают в условиях эксплуатации
колёсной пары, возникают различные дефекты.
Для обеспечения
надёжной работы на железной дороге создана система выявления дефектов колёсных
пар. Основой такой системы является выявление дефек ...
Лазерная система для измерения статистических характеристик пространственных квазипериодических структур
В последние годы наблюдается интенсивное развитие аэрокосмической и ракетной
техники, что в свою очередь ставит перед промышленностью задачу создания точных
и надежных систем связи, ориентации и обнаружения подвижных объектов в
пространстве. В большинстве случаев данные задачи решаются с прим ...