Термодинамика и закон распределения
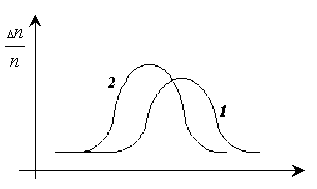
Рис.1.
А теперь по этому маршруту производят забег студенты всех курсов гражданского вуза, включая девушек. В большей массе они плохо бегают. Через некоторое время ряд студентов и студенток окажется на обочине: те же мозоли, отломались шпильки в туфлях…Другие вот-вот остановятся. Естественно, и здесь найдутся прыткие, которые убегут далеко (и в гражданском вузе имеются спортсмены)… Но и для них будет существовать такая скорость, с которой будет двигаться основная масса студентов гражданского вуза. Чем же отличаются данные забеги? В каждом забеге можно зафиксировать любые скорости (в ограниченном промежутке). Главное отличие в том, что будут разные скорости, с которыми движется большее число бегунов. График второго забега дан на Рис.1 (кривая 2 )
Данные графики описываются функциями распределения соответствующей величины (в теории вероятностей – это дифференциальная функция распределения плотности вероятностей).
С подобными законами распределения мы сталкиваемся повседневно.
При обучении преподаватель имеет дело с рядом функций распределения: распределение обучаемых по зрительному восприятию предлагаемой информации, распределение обучаемых по слуховому восприятию информации, распределение обучаемых по знаниям изучаемого предмета по техническим способностям (что является очень важным для технического вуза), по математическим способностям…
А как же тогда обучать? На каких студентов ориентироваться? Чтобы обучение проходило на научной основе, эти функции распределения следует знать. В Уссурийском филиале Дальневосточного государственного университета путей сообщения мы этим и занимаемся. Мы определяем темперамент по Айзенку и десять характеристик с выводом общего показателя интеллекта по Амгхауэру. Определяем вербальные, вычислительные, пространственные, технические способности.
Прежде всего это необходимо самим студентам. Они должны знать себя, с тем чтобы положительные качества свои усиливать, а отрицательные качества изживать из себя.
В квантовой механике в основном занимаются тем, что находят соответствующие функции распределения: функция распределения плотности вероятности нахождения частицы в соответствующих квантовых состояниях потенциальных ям: одномерной, трехмерной (твердое тело), сферической (атом, ядро) в соответствующем состоянии.
В теории измерения получаются случайные величины, которые группируются в окрестности их среднего значения (истинного значения), а в теории вероятностей они группируются в окрестности математического ожидания. Для объяснения этого можно ввести динамику: силовое поле, нелинейное взаимодействие. Нелинейное взаимодействие – воздействие системы на себя. Такое наблюдается и в общественной жизни. Стремящиеся к финишу спортсмены (особенно для получения золотой медали) сильно воздействуют друг на друга.
Общественная личность – это воздействующая на себя система. Задача обучения состоит не только в том, чтобы дать обучаемым сумму знаний, но и в том, чтобы сформировать у них стремление к самовоспитанию и самообучению, а это возможно только
Дополнительно
Кибернетика и синергетика – науки о самоорганизующихся системах
Фронт современной науки простирается от
сравнительно частных, конкретных концепций относительно различных областей
физического и химического мира, до глубочайших теорий, охватывающих различные
сферы природы, общества и технической деятельности человека. К последним
следует отнести кибернетику и ...
Структурная и молекулярная организация генного вещества
Почти полвека тому назад, в 1953 г., Д. Уотсон и Ф. Крик открыли принцип
структурной (молекулярной) организации генного вещества -
дезоксирибонуклеиновой кислоты (ДНК) [1]. Структура
ДНК дала ключ к механизму точного воспроизведения - редупликации - генного
вещества [2]. Так
возникла новая наука ...