Об одном кулисно-рычажном механизме
Смоляков Андрей Анатольевич, старший научный сотрудник РФЯЦ-ВНИИЭФ .
Уповалов Вячеслав Владимирович, научный сотрудник РФЯЦ-ВНИИЭФ .
Предлагается к рассмотрению кулисно-рычажный механизм, в котором осуществляется преобразование вращательного движения кулачка в качание кулисы. Механизм может быть реализован двумя способами, как показано на рис. 1 и 2. Устройство состоит из кулачка, вращающегося вокруг постоянной оси, и кулисы с двумя направляющими. Кулиса, с жестко заделанными направляющими, качается вдоль своей оси качания, перпендикулярной оси вращения кулачка. В каждый момент времени кулачок касается обеих направляющих (каждой в одной точке) за счет выбора формы кулачка (в первом варианте) или направляющих (во втором варианте). В первом варианте (см. рис. 1) направляющие имеют форму цилиндров, а во втором варианте (см. рис. 2) кулачок выполнен в форме цилиндра.
|
|
Для нахождения функции, описывающей форму кулачка для первого варианта, необходимо решить дифференциальное уравнение (1.1). при
l - расстояние между осями направляющих кулисного механизма; r - радиус направляющей: H - радиус качания кулисы (перпендикуляр от центра оси качания кулисы к отрезку, соединяющему центры направляющих); L - радиус вращения кулачка (между центром кулачка и центром оси вращения кулачка). |
Оси x и y лежат в плоскости определяющей кулачка и направлены соответственно вдоль максимального и минимального диаметров.
Уравнение (1.1) имеет вид дифференциального уравнения Клеро. Как известно, дифференциальное уравнение Клеро ![]() /1/ имеет особый интеграл (в параметрической форме)
/1/ имеет особый интеграл (в параметрической форме) ![]() и
и![]() , причем
, причем![]() . Правая часть дифференциального уравнения (1.1) - это
. Правая часть дифференциального уравнения (1.1) - это![]() . После подстановки имеем параметрическое решение уравнения (1.1) в виде:
. После подстановки имеем параметрическое решение уравнения (1.1) в виде:
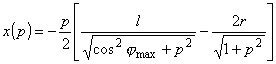
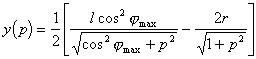
|
Для нахождения функции, описывающей форму направляющих для второго варианта (рис. 2), необходимо решить систему из 3-х уравнений (2.1), (2.2) и (2.3), приведенных ниже. Уравнение (2.1) определяет, что каждая точка направляющей лежит на окружности - кулачке. Дифференциальное уравнение (2.2) определяет, что в точках соприкосновения кулачка и направляющих совпадают производные, т.е. происходит касание. Уравнение (2.3) (следует из
|
|
при очевидных граничных условиях
![]() и
и ![]() , где
, где
![]() - максимальный угол отклонения кулисного механизма с направляющими вокруг оси качания кулисы;
- максимальный угол отклонения кулисного механизма с направляющими вокруг оси качания кулисы;
![]() - угол отклонения кулисного механизма с направляющими вокруг оси качания кулисы;
- угол отклонения кулисного механизма с направляющими вокруг оси качания кулисы;
![]() - угол поворота кулачка вокруг оси собственного вращения при отклонении кулисы на угол
- угол поворота кулачка вокруг оси собственного вращения при отклонении кулисы на угол![]() ;
;
l - расстояние между осями направляющих кулисного механизма;
R - радиус кулачка;
H - радиус качания кулисы (перпендикуляр от центра оси качания кулисы к отрезку, соединяющему центры направляющих);
L - радиус вращения кулачка (между центром кулачка и центром оси вращения кулачка).
Ось x направлена вдоль центральной оси направляющей, ось y - перпендикулярно к оси x. Начало координат - середина направляющей, самое ?узкое¦ место. Координата y определяет радиус сечения направляющей в точке с координатой x. Продифференцируем (2.1) по x:
Дополнительно
Развитие представлений о природе тепловых явлений и свойств макросистем
Вокруг нас происходят явления, внешне весьма
косвенно связанные с механическим движением. Это явления, наблюдаемые при
изменении температуры тел, представляющих собой макросистемы, или при переходе
их из одного состояния (например, жидкого) в другое (твердое либо
газообразное). Такие явления наз ...
Есть ли жизнь на Марсе
«Есть ли жизнь на
Марсе, нет ли жизни на Марсе - науке неизвестно» - это не просто удачный
афоризм из популярной кинокомедии «Карнавальная ночь», который широко вошел в
наш разговорный язык и стал ходячей шуткой. Главное здесь в том, что эта фраза
очень долгое время отражала наш действитель ...
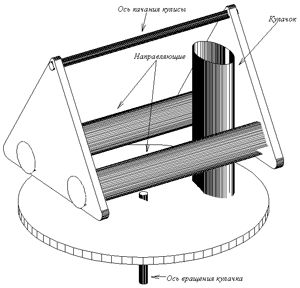 Рис. 1.
Рис. 1. 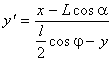 (2.2)
(2.2) 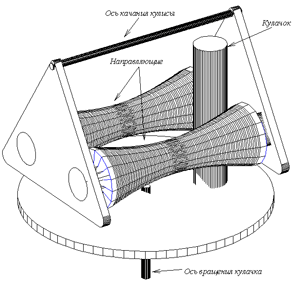 Рис. 2.
Рис. 2.