Об одном кулисно-рычажном механизме
(2.4)
из (2.2)
, подставим в (2.4)
, отсюда следует
, и имеем
(2.5) из (2.3) следует, что
или 
, - подставляем в (2.5)
, что дает
(2.6) Подставим из (2.3) выражение для
в (2.6)
или
, откуда имеем
(2.7) Подставив (2.7) в (2.2), получим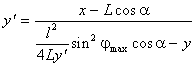
или
или
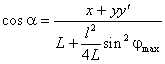(2.8) Подставив из (2.8) выражение для 
в (2.7), получим
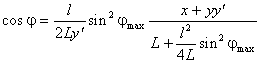(2.9) Подставим (2.8) и (2.9) в (2.1), получим выражение:
,
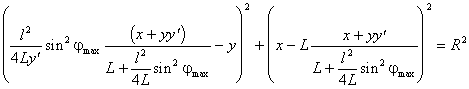в котором приведем к общему знаменателю выражения в скобках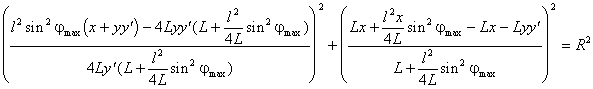 
и затем сократим выражения в скобках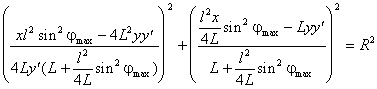
,
что приведет к окончательному виду дифференциального уравнения, определяющего форму направляющих
(2.10) Если обозначить
и 
, то уравнение (2.10) можно переписать как
(2.11) Уравнение (2.11) преобразуем так, чтобы получить дифференциальное уравнение Лагранжа /1/.
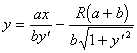(2.12) Как известно, дифференциальное уравнение Лагранжа 
приводится к уравнению в виде 
;
переписав последнее относительно
в виде 
(2.13) и получаем линейное дифференциальное уравнение относительно.
Для уравнения (2.12) можно записать соотношения
, 
, 
, 
.
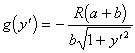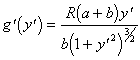Обозначим 
и запишем уравнение (2.13) как линейное дифференциальное уравнение относительно
.
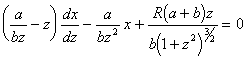(2.14) Обозначим 
и перепишем уравнение (2.14) как линейное дифференциальное уравнение первого порядка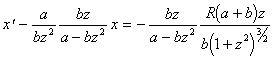
,
или, после упрощения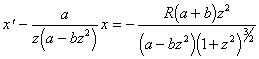 
(2.15) Как известно, линейное дифференциальное уравнение первого порядка 
при интегральном множителе 
имеет общее решение
.
Для уравнения (2.15) можно записать
, 
.
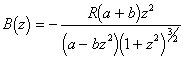Из /2/ имеем:
,
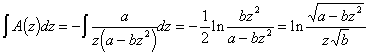отсюда
.
Дополнительно
Спутниковая связь
Современные
организации характеризуются большим объемом различной информации, в основном
электронной и телекоммуникационной, которая проходит через них каждый день.
Поэтому важно иметь высококачественный выход на коммутационные узлы, которые
обеспечивают выход на все важные коммуникационные линии. ...
Лазерная система для измерения статистических характеристик пространственных квазипериодических структур
В последние годы наблюдается интенсивное развитие аэрокосмической и ракетной
техники, что в свою очередь ставит перед промышленностью задачу создания точных
и надежных систем связи, ориентации и обнаружения подвижных объектов в
пространстве. В большинстве случаев данные задачи решаются с прим ...