Математическая модель измерительной системы
Оптическая система КОС, выполненная по схеме “входной транспарант перед фурье-объективом”, состоит из ряда последовательно расположен-ных вдоль оптической оси узлов: источник когерентного излучения, входной транспарант, фурье-объектив, фоторегистратор спектра (рис.2).
В такой системе, для получения высококонтрастного и сфокусирован-ного изображения исследуемого сигнала, источником когерентного излу-чения является точечный источник, излучаемое поле которого описывается функцией: 
(5.1), где А0-амплитуда световой волны источника; 
- дельта-функция Дирака. Кроме того, в оптике принято считать источник точечным, если его размеры в десять и более раз меньше растояния до оптической системы, что обычно всегда имеет место на практике для КОС.
Тогда, распределение поля 
в плоскости х1у1 согласно принципу Гюйгенса-Френеля, будет описываться выражением :
(5.3), где 
- оператор преобразования Френеля ; СФ- комплексная постоянная, равная 
. Если в плоскости х1у1 помещен пространственный транспарант с амплитудным коэфициентом пропускания 
, являюшийся записью исследуемого сигнала, то распределение поля за транспарантом может быть описано как
(5.2).
Применив принцип Гюйгенса-Френеля (5.3), можно определить распре-деление светового поля в плоскости х2у2 перед фурье-объективом, а поле за ним - применив (5.2).
Таким образом, распределение поля в плоскости х3у3 анализа будет описываться :
(5.4), где 
- оператор Френеля для преобразования поля на i-м участке свободного пространства толщиной li.
Рассмотрим последовательно распостранение когерентной световой волны в оптической системе КОС, представленной на рис. 2.
Подставив (5.1) в (5.3), определим распределение светового поля во входной плоскости х1у1 перед транспарантом
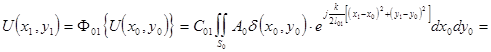
, где 
(5.5).
Выражение (5.5) получено с использованием фильтрующего свойства дельта-функции и описывает расходящуюся сферическую волну в плоскости х1у1 перед входным транспарантом в параксиальном приближении. Исполь-зование фильтрирующего свойства -функции допустимо в силу прост-ранственной инвариантности рассматриваемой параксиальной области оптической системы. Такое допущение обычно всегда имеет место на прак-тике, поскольку для уменшения влияния аберраций оптической системы на качество фурье-образа, используют лишь ее центральную часть - парак-сиальную область.
Определив распределение поля за входным транспарантом c ис-пользованием (5.2), поле во входной плоскости фурье-объектива, согласно принципу Гюйгенса-Френеля, можно представить как
Дополнительно
Есть ли жизнь на Марсе
«Есть ли жизнь на
Марсе, нет ли жизни на Марсе - науке неизвестно» - это не просто удачный
афоризм из популярной кинокомедии «Карнавальная ночь», который широко вошел в
наш разговорный язык и стал ходячей шуткой. Главное здесь в том, что эта фраза
очень долгое время отражала наш действитель ...
Термоиндикаторы
Роль
температурных и тепловых измерений настолько велика, что в настоящее время без
них не может обойтись практически ни одна область знаний, ни одна отрасль
промышленности.
Каждый
из существующих способов измерения температуры имеет свои достоинства и
недостатки, поэтому выбор того или ин ...