Расчетная часть
Применив принцип Гюйгенса-Френеля (5.3), можно определить распре-деление светового поля в плоскости х2у2 перед фурье-объективом, а поле за ним - применив (5.2).
Таким образом, распределение поля в плоскости х3у3 анализа будет описываться :
, где 
- оператор Френеля для преобразования поля на i-м участке свободного пространства толщиной li.
Распределение поля в плоскости х2у2 за фурье-объективом, согласно (5.2) будет
, а подставив (5.6) в (5.7) с учетом (5.3), распределение поля в плоскости х3у3 анализа можно представить в виде :
,
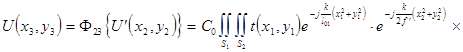
где 
.
Учитывая (5.16) и (5.20) выражение (5.14) можно представить в виде:
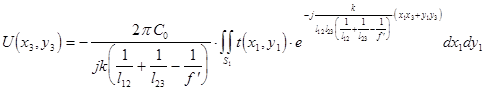(5.23),
откуда видно, что квадратичные фазовые искажения фурье-образа (5.14) сигнала устранимы не только при освещении входного транспаранта плос-кой, но и сферической волной при выполнении условий (5.18 ) и (5.22).
Выходной электрический сигнал ФИС представляет собой решение известной в оптике задачи о набегании светового пятна, распределение освещенности в котором описывается выражением:
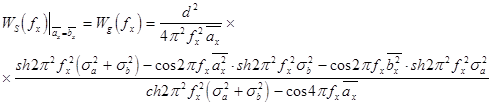, на узкую щеле-вую диафрагму вдоль координаты х3. Наиболее общим методом решения подобных задач является вычисление интеграла свертки функции освещенности с функцией 
пропускания полевой диафрагмы ФИС, равной:
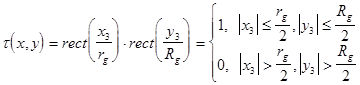(5.24), где 
- ширина щели вдоль координаты х3, 
- высота щели вдоль координаты у3.
Распределение 
комплексных амплитуд световой волны в плос-
кости х3у3 анализа КОС описывается выражением (5.23) и является прост-ранственно-частотным фурье-образом входного сигнала 
т.е.
.
Из уравнений Максвелла для электромагнитной волны следует, что энергия преносимая волной, пропорциональна квадрату амплитуды напря-женности электромагнитного поля, т.е.
(5.25), где К - постоянный коэфициент, зависящий от свойств среды, где распостраняется электромагнитная волна [14, 23]. Поэтому пространственно-частотный энергетический спектр 
входного сигнала пропорционален распределению освещенности 
в плоскости спектрального анализа КОС, т.е.
(5.26), где 
,
- взаимосвязь между пространственными х(у) и пространственно-частотными 
координатами в плоскости спектрального анализа КОС; 
комплексная постоянная, определяемая (5.8).
Дополнительно
Конструкции и технология изготовления электротехнических изделий
Настоящее методическое
пособие предназначено для студентов Института Электротехники, выполняющих
курсовые и дипломный проекты (КП и ДП), и призвано оказать им помощь по
выполнению конструкторско-технологической части проектов.
В связи с введением Единой
системы конструкторской документации (ЕСК ...
Ремонт колесных пар
Из-за больших
статических и динамических нагрузок, которые возникают в условиях эксплуатации
колёсной пары, возникают различные дефекты.
Для обеспечения
надёжной работы на железной дороге создана система выявления дефектов колёсных
пар. Основой такой системы является выявление дефек ...