TechStandard

Кинематический расчет исследуемой конструкции

(3.36)

В полученном выражении (3.35) произведём подстановки:

(3.38)

(3.37)

(3.39)

Очевидно, что выражение (3.35) имеет форму квадратного трёхчлена:

,

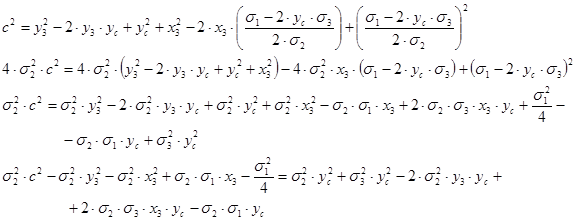
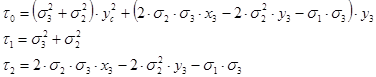
откуда:

(3.40)

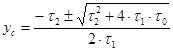
Избыточный корень отсекается по условию физической осуществимости.

Аналогичным образом поступим при определении координаты центра ведущего колеса по оси абсцисс:

(3.43)

(3.42)

(3.41)

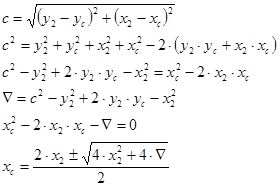
3.3.3 Определение координат шарниров упругих элементов колеса в любой момент времени

Для построения модели работы ведущего колеса с внутренним подрессориванием необходимо определить, какое положение в каждый момент времени занимает каждый из упругих элементов системы подрессоривания. колеса. Первым шагом на пути решения этой задачи является определение координат точек шарниров упругих элементов.

Исходные данные:

(3.44)

закон изменения профиля поверхности:

максимальное смещение зубчатого обода относительно оси вращения колеса:

(3.45)

Дополнительно

Проектирование технологии ремонта гидроцилиндров с использованием полимерных материалов
Одно из направлений повышения эффективности производства - его переоснащение современной техникой, внедрение передовых технологических процессов и достижений современной науки. В лесной промышленности и лесном хозяйстве таким направлением наряду с увеличением единичной мощности выпускаемой те ...

Эволюция биологических механизмов запасения энергии
В основу эволюционной концепции биоэнергетики положена гипотеза о том, что на заре становления жизни адениновая часть АДФ и АДФ-со-держащих коферментов использовалась в качестве антенны, улавливающей ультрафиолетовый свет, который в те времена достигал поверхности океана. Поглощение ультрафиолета ...