Классификация объектов нечисловой природы на основе непараметрических оценок плотности
для любого 
Функция называется производной Родона-Никодима меры 
по мере 
, а в случае, когда - вероятностная мера, также плотностью вероятности по отношению к . " [5]
Будем считать, что в пространстве объектов нечисловой природы фиксирована некоторая мера , а мера соответствует распределению Р случайного элемента 
со знаниями в измеримом пространстве 
, т. е.
Если - 
пространство из конечного числа точек, то в качестве меры можно использовать считающую меру (приписывающую единичный вес каждой точке), т. е. 
, или
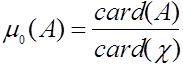
В случае считающей меры значение плотности в точке совпадает с вероятностью попасть в точку , т. е. 
Многие методы классификации используют расстояния или меры близости между объектами или признаками. Такие методы пригодны и для классификации объектов нечисловой природы, лишь бы в соответствующем пространстве было определено расстояние или мера близости. Таким образом, широко известные иерархические агломеративные алгоритмы ближайшего соседа, дальнего соседа, средней связи и др., результатом работы которых являются дендрограммы, на самом деле относятся к статистике объектов нечисловой природы.
Не пытаясь рассмотреть все многообразие методов классификации в статистике объектов нечисловой природы (см., например, [6, 7]), сосредоточимся на тех из них, которые используют плотности распределения и их оценки. Зная плотности распределения классов, можно решать основные задачи классификации - как задачи выделения кластеров, так и задачи диагностики. В задачах кластер-анализа можно находить моды плотности и принимать их за центры кластеров или за начальные точки итерационных методов типа динамических сгущений. В задачах диагностики (дискриминации, распознавания образов с учителя) можно принимать решения о классификации объектов на основе отношения плотностей, соответствующих классам. При неизвестных плотностях представляется естественным использовать их состоятельные оценки. Корректность такой постановки, как правило, нетрудно обосновать, например, в стиле [8]. Таким образом, для переноса на пространства произвольной природы основных методов классификации рассматриваемого типа достаточно уметь оценивать плотность распределения вероятности в таких пространствах.
Дополнительно
Спутниковая связь
Современные
организации характеризуются большим объемом различной информации, в основном
электронной и телекоммуникационной, которая проходит через них каждый день.
Поэтому важно иметь высококачественный выход на коммутационные узлы, которые
обеспечивают выход на все важные коммуникационные линии. ...
Современный прокатный стан
Современный
прокатный стан представляет собой технологический комплекс последовательно
установленных машин, используемых для получения прокатных изделий заданных
размеров с необходимыми качественными показателями. Производительность
прокатного стана определяется пропускной способностью отдельных а ...