Классификация объектов нечисловой природы на основе непараметрических оценок плотности
Методы оценивания плотности вероятности в пространствах общего вида предложен и первоначально изучены в [4]. В частности, в задачах классификации объектов нечисловой природы предлагаем использовать непараметрические ядерные оценки плотности типа Парзена-Розенблатта (этот вид оценок и его название введены нами в [4]):
,
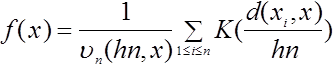где К: 
- ядерная функция 
- выборка по которой оценивается плотностью, 
- расстояние между элементом выборки 
и точкой 
, в которой оценивается плотность последовательность 
показателей размытости такова, что при 
0 и n
, а 
- нормирующий множитель, обеспечивающий выполнение условия
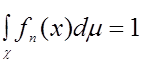
Оценки типа Парзена-Розенблатта - частный случай линейных оценок [4]. В теоретическом плане они выделяются тем, что удается получать результаты такого же типа, что в классическом одномерном случае (
), но, разумеется, с помощью совсем иного математического аппарата.
Одна из основных идей состоит в том, чтобы согласовать между собой расстояние 
и меры 
. А именно, рассмотрим шары радиуса 
и их меры
Предположим, что 
как функция 
при фиксированном непрерывна и строго возрастает. Введем функцию
Это - монотонное преобразование расстояния, а потому 
- метрика или симметрика (т. е. неравенство треугольника может быть не выполнено), которую, как и 
, можно рассматривать как меру близости между и 
.
Введем
.
Поскольку 
определена однозначно, то
^
где 
., а потому
Переход от к 
напоминает классическое преобразование, использованное Н. В. Смирновым, 
, переводящее случайную величину 
с непрерывной функцией распределения 
в случайную величину 
, равномерно распределенную на [ 0, 1]. Оба рассматриваемых преобразования существенно упрощают дальнейшие рассмотрения.
Дополнительно
Достижения генной инженерии и биотехнологии
В
своей работе я раскрываю тему достижений генной инженерии и биотехнологии.
Возможности, открываемые генетической инженерией перед человечеством как в
области фундаментальной науки, так и во многих других областях, весьма велики
и нередко даже революционны. Так, она позволяет осуществлять инду ...
Порошковая металлургия и дальнейшая перспектива ее развития
Порошковой металлургией
называют область техники, охватывающую совокупность методов изготовления
порошков металлов и металлоподобных соединений, полуфабрикатов и изделий из них
или их смесей с неметаллическими порошками без расплавления основного
компонента.
Из имеющихся разнообразных
способов ...