Классификация объектов нечисловой природы на основе непараметрических оценок плотности
ПРИМЕР 2. Рассмотрим пространство функций 
, определенных на конечном множестве 
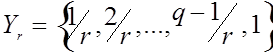со значениями в конечном множестве 
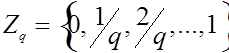. Это пространство можно интерпретировать как пространство нечетких множеств [11]. Очевидно, 
. Будем использовать расстояние 
. Непараметрическая оценка плотности имеет вид: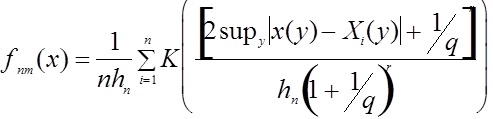 
.
Если 
, 
, то при 
выполнены условия теоремы 3, а потому справедливы теоремы 1 и 2.
. ПРИМЕР 3. Рассматривая пространства ранжировок 
объект непреов, в качестве расстояния 
между ранжировками 
и 
. Тогда 
. не стремиться к 0 при 
., условия теоремы 3 не выполнены.
Пространства разнотипных признаков - это декартово произведение непрерывных и дискретных пространств. Для него возможны различные постановки. Пусть, например, число градаций качественных признаков остается постоянным. Тогда непараметрическая оценка плотности сводится к произведению частоты попадания в точку в пространстве качественных признаков на классическую оценку Парзена-Розенблатта в пространстве количественных переменных. В общем случае расстояние 
можно, например, рассматривать как сумму евклидова расстояния 
между количественными факторами, расстояния 
между номинальными признаками (
, если 
и , если 
) и расстояния 
между порядковыми переменными (если 
и 
- номера градаций., то 
.
Наличие количественных факторов приводит к непрерывности и строгому возрастанию 
, а потому для непараметрических оценок плотности в пространствах разнотипных признаков справедливы теоремы 1 - 3.
Дополнительно
Конструкции и технология изготовления электротехнических изделий
Настоящее методическое
пособие предназначено для студентов Института Электротехники, выполняющих
курсовые и дипломный проекты (КП и ДП), и призвано оказать им помощь по
выполнению конструкторско-технологической части проектов.
В связи с введением Единой
системы конструкторской документации (ЕСК ...
Крепление кабелей
Анализ качества работ по монтажу СКС показывает, что иногда подрядчики
неудовлетворительно относятся к соблюдению правил укладки и крепления кабеля.
Чаще всего подобная небрежность свойственна организациям, чья прежняя
специализация состояла в монтаже АТС - при работе с телефонным кабелем
(Категор ...