Классификация объектов нечисловой природы на основе непараметрических оценок плотности
Преобразование 
зависит от точки 
, что не влияет на дальнейшие рассуждения, поскольку ограничиваемся изучением сходимости в точке.
Функцию 
, для которой мера шара радиуса 
равна , называют [4] естественным показателем различия или естественной метрикой. В случае пространства 
и евклидовой метрики 
имеем
где 
-объем шара единичного радиуса в .
Поскольку можно записать, что
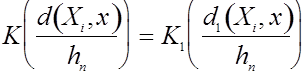
где
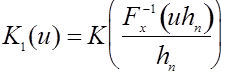
то переход от к 
соответствует переходу от 
к 
. Выгода от такого перехода заключается в том, что утверждения приобретают более простую формулировку.
ТЕОРЕМА 1. Пусть - естественная метрика,
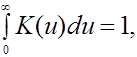
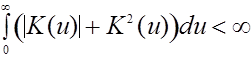
Плотность 
непрерывна в и ограничена на 
, причем 
. Тогда 
, оценка 
является состоятельной, т. е. 
по вероятности при 
,
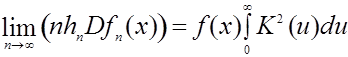
Теорема 1 доказана в [4]. Однако остается открытым вопрос о скорости сходимости ядерных оценок, т. е. о поведении величины
и об оптимальном выборе показателей размытости 
.
Введем круговое распределение 
и круговую плотность 
.
ТЕОРЕМА 2. Пусть ядерная функция 
непрерывна и 
при 
. Пусть круговая плотность допускает разложение
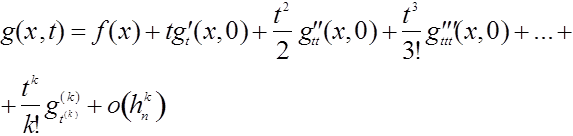
причем остаточный член равномерно ограничен [0, 1, , 
]. Пусть
Дополнительно
Становление детской журналистики и её влияние на психологию ребёнка
Русская пресса для юного читателя в
отличие от «взрослой» началась с журнала.
Детская журналистика в нашей стране
имеет богатую историю. До революции, в основном в Петербурге и Москве,
издавалось около трехсот детских и юношеских журналов. Одни из них выходили
десятилетиями, другие прекращали ...
Оборудование для механического обезвоживанья и сушки текстильных материалов
Сушка является самым распространенным технологическим
процессом красильно-отделочного производства. На многих отделочных фабриках
сушильное оборудование занимает приблизительно до 30 % производственных
площадей, потребляет до 40 % всего расходуемого тепла и до 30 % электроэнергии.
Одним из эффек ...