Классификация объектов нечисловой природы на основе непараметрических оценок плотности
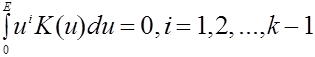
Тогда
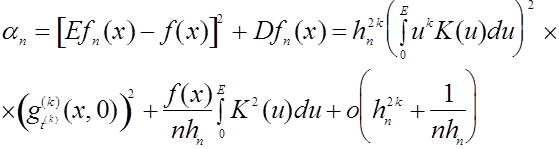
Величина 
достигает минимума, равного
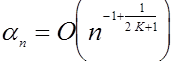
при
что совпадает с классическими результатами для 
(см. [9, с316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра 
.
В случае дискретных пространств естественных метрик не существует. Однако можно получить аналоги теорем 1 и 2 переходя к пределу не только по объему выборки 
, но и по параметру дискретности 
.
Пусть 
- последовательность конечных пространств, 
- расстояния в 
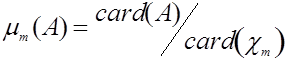для любого 
.
Положим
,
,
,
Тогда функции 
кусочно постоянны и имеют скачки в некоторых точках 
, причем 
.
ТЕОРЕМА 3. Если 
при 
(другими словами, 
при ), то существует последовательность параметров дискретности 
такая, что при 
, , 
справедливы заключения теорем 1 и 2.
ПРИМЕР 1. Пространство 
всех подмножеств конечного множества 
из элементов допускает [10, Пар 4. 3] аксиоматическое введение метрики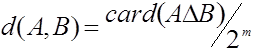 
, где 
- символ симметрической разности множеств. Рассмотрим непараметрическую оценку плотности типа Парзена - Розенблатта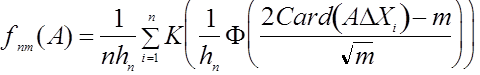 
, где 
- функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 3 
.
Дополнительно
Крепление кабелей
Анализ качества работ по монтажу СКС показывает, что иногда подрядчики
неудовлетворительно относятся к соблюдению правил укладки и крепления кабеля.
Чаще всего подобная небрежность свойственна организациям, чья прежняя
специализация состояла в монтаже АТС - при работе с телефонным кабелем
(Категор ...
Становление детской журналистики и её влияние на психологию ребёнка
Русская пресса для юного читателя в
отличие от «взрослой» началась с журнала.
Детская журналистика в нашей стране
имеет богатую историю. До революции, в основном в Петербурге и Москве,
издавалось около трехсот детских и юношеских журналов. Одни из них выходили
десятилетиями, другие прекращали ...